En el capítulo de hoy hablaremos sobre el descenso por gradiente, un algoritmo de optimización que juega un papel clave en el campo del Machine Learning. Tal y como mencionamos en capítulos anteriores, «Redes Neuronales y Deep Learning. Capítulo 2: La Neurona» y «Redes Neuronales y Deep Learning. Capítulo 1: Preludio», una neurona puede verse como una función matemática que recibe unos valores de entrada y arroja un valor de salida. Además, vimos también que esos valores que reciben se ven afectados por unos parámetros o pesos. Estos parámetros determinan la influencia que tiene un valor de entrada en la función. De esta manera, dichos pesos tienen una importancia directa en el error que pueda tener nuestra red neuronal en sus predicciones. Es aquí donde entra en juego la función de coste, que es aquella que trata de cuantificar el error entre la predicción arrojada y el valor real, con el fin de optimizar los parámetros de la red neuronal. Mediante el descenso por gradiente trataremos de minimizar dicha función de coste tal y como explicaremos a continuación.
Optimización: Gradiente de una función
Como hemos visto en el apartado anterior nuestra misión en lo que sigue será encontrar el valor mínimo de la función de coste. Encontrar el mínimo de una función es una tarea muy común en el análisis matemático. Normalmente, la forma común de atacar el problema de encontrar el punto mínimo se reduce a encontrar el punto (o los puntos) en los que la derivada de la función es igual a cero. De hecho, es relativamente fácil cuando nos encontramos con funciones convexas como la siguiente:
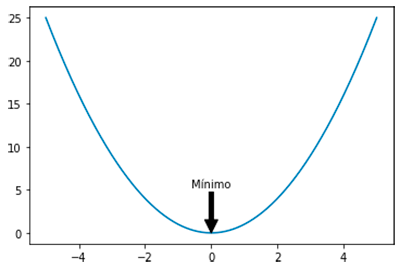
Sin embargo, en la mayoría de los casos nos encontraremos con funciones de dimensiones altas y de mayor complejidad. En estos casos encontrar el mínimo puede resultar una tarea bastante tediosa ya que implica la resolución de un número presumiblemente alto de derivadas parciales. Esto ocurre, por ejemplo, en el siguiente caso:
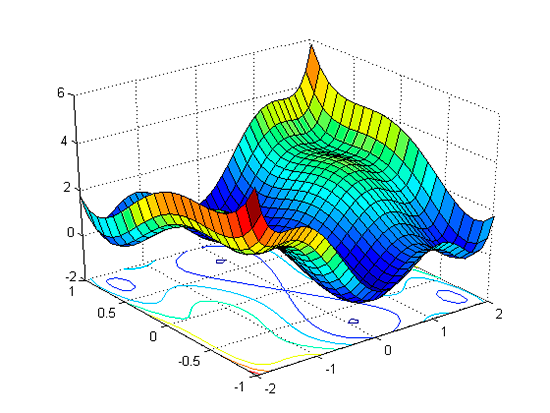
No obstante, no está todo perdido. En este punto es donde el gradiente de la función entra en juego.
Definición: Llamamos gradiente o vector gradiente de una función a la generalización vectorial de la derivada. Se trata de un vector de igual dimensión que dicha función.
«Es también conveniente recordar que la derivada contiene información sobre la pendiente de nuestra función. Concretamente nos dice la dirección de máximo crecimiento de la misma. Presentamos entonces la fórmula del gradiente de una función f con n parámetros x1, …, xn«
Lógica del descenso por gradiente
Ahora que ya sabemos que el gradiente de una función contiene información sobre la pendiente de dicha función en un punto, es momento de ilustrar la lógica del algoritmo mediante un ejemplo clásico.
Supongamos que nos encontramos en un punto aleatorio de una cordillera con varias montañas de diferente altura donde la visibilidad es nula. Nos hemos perdido y queremos regresar al punto más bajo del valle, pero la niebla hace imposible la visión. Quizá en tal situación la solución más inteligente es la siguiente:
- Detectar la dirección en la que más se desciende. Podríamos dar un paso en cada una de las cuatro direcciones para finalmente elegir aquella en la que más altura estamos descendiendo. En la práctica esto es análogo a calcular el gradiente, ya que mediante este podemos detectar la dirección de máximo crecimiento y, consecuentemente, la de máximo decrecimiento.
- Una vez hemos detectado la dirección de decrecimiento andamos uno o varios pasos en ese sentido.
De esta manera repetimos ambas operaciones hasta llegar al punto mínimo. Pero, hay una cuestión importante… ¿Cómo de grandes han de ser los pasos que demos en cada iteración? Es aquí donde aparece el concepto de Learning Rate.
Learning Rate
Como hemos comentado, podemos entender el Learning Rate como aquel parámetro que indica cuán largos han de ser los pasos que demos mientras descendemos. De manera técnica esto se traduce en cuánto afecta el gradiente a la actualización de nuestros parámetros.
A priori, parece razonable seguir la siguiente estrategia:
- Si el gradiente nos indica que la pendiente es elevada entonces daremos un paso muy largo para aprovechar y descender lo máximo posible.
- Si el gradiente nos indica que la pendiente es poco pronunciada daremos un paso más corto.
En conclusión, daremos un paso en forma proporcional al gradiente, pero para controlar dicha proporción usaremos el learning rate.
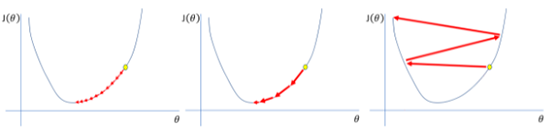
En las siguientes imágenes podemos observar que ocurre en el algoritmo de descenso por gradiente para una misma función de coste pero diferentes valores de learning rate:
- Un learning rate muy pequeño, como el de la figura de la izquierda puede hacernos converger al mínimo, pero conlleva un alto número de pasos. Esto en la práctica se traduce en un alto costo computacional ya que quiere decir que tendremos que realizar una gran cantidad de derivadas. Además, un learning rate pequeño puede hacernos converger a mínimos locales en lugar de mínimos absolutos.
- Un learning rate demasiado alto, como el de la figura de la derecha puede hacernos diverger. Los pasos son tan largos que se hace muy difícil introducirnos en la zona de mínimo coste.
Quizá lo veamos más claro en la siguiente animación que ilustra además la diferencia entre las distintas técnicas más usadas en la actualidad que permiten ajustar el learning rate de forma dinámica.
Llegados a este momento estamos preparados para a aprender cómo dotar a una red neuronal de esa inteligencia o capacidad de reajustar sus parámetros. Pero, ¡eso será en el próximo capítulo!