Sin duda uno de los problemas más recurrentes en la historia de la informática se trata del procesamiento y análisis de imágenes. Es decir, dotar a las máquinas de “ojos” que les permitan comprender el entorno que las rodea y tomar decisiones en función al medio. Este campo de estudio recibe el nombre de visión por ordenador o visión artificial y las redes neuronales convolucionales, RNC en lo que sigue, cobran una importancia vital en él ya que son especialistas en trabajar con imágenes.
Este tipo de redes salieron a la luz en 1998 de la mano de un artículo de Yann LeCun en el que se asentaron las bases de la idea intuitiva que presentaremos a continuación.
¿Cómo funcionan las redes neuronales convolucionales?
Bien, hemos comentado que las redes neuronales convolucionales son tremendamente útiles cuando trabajamos con imágenes. Por ello, para entender su funcionamiento es conveniente entender la lógica de la visión humana y eso es lo que haremos a continuación.
Estoy completamente seguro de que la totalidad de los lectores han sido capaces de reconocer un coche en la anterior imagen ¿y si fuera rojo en vez de amarillo? ¿si fuera más moderno? ¿si fuera todoterreno? En cualquier caso la respuesta es que siempre sabremos reconocer un coche, ¿por qué? Aquí está el kit de la cuestión. Nuestro cerebro ha aprendido que existen una serie de elementos que conforman un coche: ruedas, chasis, retrovisores, faros… y que siempre son comunes. Y aún más allá, podemos seguir extendiendo dicha lógica de manera recursiva a cada uno de los elementos. Por ejemplo, hemos aprendido que una rueda es redonda y tiene una llanta, que los retrovisores son espejos que se sitúan justo a las puertas delanteras…
Este aprendizaje segmentado es lo que trata de emular una RNC. Además, se acopla perfectamente a la propia naturaleza de la red, ya que como vimos en capítulos anteriores una red tiene diferentes capas que pueden ser interpretadas como etapas de reconocimiento visual. Por ejemplo, en las primeras capas la red puede centrarse en distinguir formas geométricas, en la segunda capa asociar círculos a ruedas, rectángulos a cristales… y en las últimas capas decidir si se han detectado elementos suficientes para clasificar la imagen como coche o no.
Hasta aquí la parte intuitiva, ahora nos adentraremos en la parte más técnica.
Las matemáticas detrás de las RNC
Llegados a este punto tenemos que entender que una imagen, a priori, no es más que una matriz binaria de píxeles. En la matriz encontraremos un 1 en las posiciones en las cuales existan trazos y un 0 en las que no, tal y como vemos a continuación. Además, una matriz es fácilmente “aplanable” en un vector si ponemos por ejemplo todas las filas una tras otra. De esta forma hemos convertido una imagen en un vector, que sí es algo consumible por una RNC.
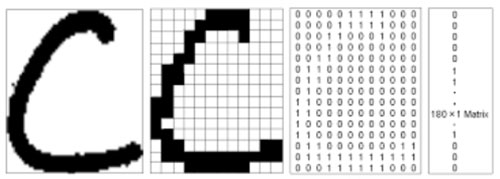
Cabe mencionar que esto es así cuando la imagen es en blanco y negro. Cuando es una imagen en color la matriz se transforma en tres, una correspondiente a cada uno de los colores RGB, pero básicamente la idea sería la misma.
Ahora bien, si nos fijamos, el valor de un píxel siempre estará estrechamente relacionado con el de su píxel vecino. Es aquí donde entran en juego los conceptos de convolución y filtro.
Una convolución no es más que una operación que generará una nueva matriz a partir de una dada. Para ello aplicará a la matriz un filtro que básicamente generará un nuevo píxel a partir de la combinación de operaciones matemáticas entre el píxel original y sus vecinos más cercanos. De esta forma, si desplazamos el filtro por toda nuestra imagen podremos obtener un resultado como los que se presentan a continuación.

Como podemos observar, existen muchos tipos de filtro: para detectar bordes verticales, bordes horizontales, para implementar desenfoques… De hecho los valores que puede tomar este filtro son infinitos y cada uno de ellos aportará algo diferente. Pero… ¿Tenemos entonces que elegir nosotros esos valores? La respuesta es que no. Como vimos en el capítulo anterior «Redes Neuronales y Deep Learning. Capítulo 4: Backpropagation», somos capaces de dotar a la red de autonomía para aprender. En este caso dicha cualidad nos permite que la red aprenda qué valores y en general que filtros son los más idóneos para detectar características comunes a nuestro objeto de clasificación.
Hasta aquí las matemáticas por hoy. En lo que sigue trataremos, entre otros temas, las aplicaciones más curiosas de estas redes ¡no te lo pierdas!












