In recent articles we have talked about analysing documents without reading them, as well as the use cases that can be given to a tool of this type. One of the applications discussed in that first article was state-of-the-art classification, but what exactly does this mean? We will now try to explain it by means of an example:
Let us suppose a librarian whose library has just opened a new section for chemistry books. The librarian, lacking the necessary training to know the different sub-subjects present in this discipline, is nevertheless obliged to provide the shelves with a certain structure instead of just placing the books randomly. This is precisely the problem addressed by the classification of the state of the art. That is to say, without knowing anything about the different subjects present in the documents we have in our hands, we are able to classify them. This classification is done on the basis of the similarity of the texts.

This is the basic idea of the problem, but there are many important issues worth commenting on, so let's get down to it.
In how many groups do we classify our documents?
Continuing with the example given in the previous section, we can find two cases.
Predefined number of groups
Let's assume that the librarian has only one shelf to classify his chemistry books. Moreover, the shelf consists of exactly five shelves. The librarian, neat and meticulous, decides to follow the format of the rest of the library: one shelf per subject, in turn divided into five further subcategories. In this case, it is clear that the classification of texts should be confined exclusively to these five classes. In this way, and along the lines of what we mentioned earlier, we must force our algorithm to find five groups in which to classify the texts, so that the documents belonging to the same group are the most similar to each other. At this point, there are three possibilities:
- All texts are very similar to each other, so five groups are too many subdivisions.
- The texts are so different that more than five categories are needed. Otherwise we would find texts of very different kinds in the same category.
- Five is the optimal number of groups based on the variance of the documents.
No restrictions on the number of groups
The second option is that the librarian has several shelves available, so he/she has no initial restriction on the number of groups in which to classify the books. This time, the most convenient thing to do before choosing the number of groups is to perform an optimisation of this parameter. For this purpose we have several options:
- Trial and error, together with mathematics and computational skills, until we are happy with the resulting groups. In this case, the librarian should read the books as he/she has time (which in practice translates as computing power). In this way he/she will have an overview of how well formed the groups are (which in practice translates into assigning a coherence metric). In this way, after trying several groupings, he could select the best one.
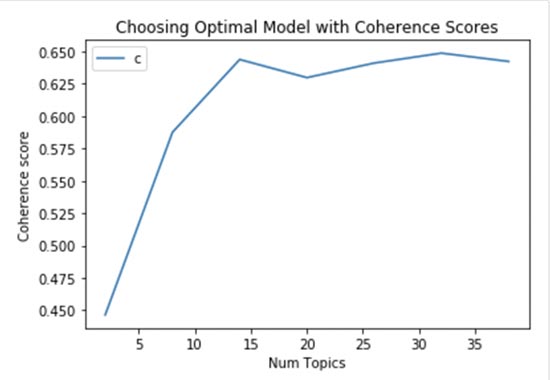
- Business knowledge. Our librarian may not have the faintest idea about chemistry, but he happens to be a genius in both physics and mathematics. His experience tells him that in this type of science there are always more than 8 subcategories, but never more than 14. Or you have no idea about science in general, but your colleague in a nearby bookshop has already gone through the trouble of sorting out the chemistry section and recommends a certain number of subcategories.
Can a book belong to more than one group?
The answer is yes. In reality, our state-of-the-art classification algorithm will not result in the group to which the text belongs, but rather in the probability of belonging to each group. From there, the most common thing to do is to associate the text with the group to which it is most likely to belong, but there could be circumstances such as the following:
- The probability of belonging to several groups is very similar. This is especially true when we have a small number of groups to classify into. In this case the librarian could either label the book with both labels or opt for one of them, knowing that either classification is equally accurate (or inaccurate).
- None of the probabilities is high enough to decide to classify the book in a group with any confidence. In this case, if this were the case for many of the books, the librarian might consider establishing some further grouping, for example with the label "other" or "miscellaneous".
How do we know what the theme of each group is?
Once we have the texts sorted into the agreed number of groups, the librarian will have to put a label on each shelf indicating the subject matter. A clever strategy for an individual might be to simply read the synopses and titles of the books in each group. In this sense it would make sense to find keywords and matches that can help establish the subject matter. Something similar happens with our algorithm, which is based on finding the most characteristic words of each group as well as the most representative texts of them. In this way, at a glance, we will be able to put a label after the creation of the groups.
And on a technical level... what are we using?
In our last blog post on this topic, The 5 W's of document analysis, we discussed the term NLP. While it is true that natural language processing is the key field of work for classification according to the state of the art, today we will go a step further and introduce the algorithm we have focused on to develop this application.
Latent Dirichlet Allocation(LDA):
This is an unsupervised learning algorithm that allows documents to be represented in different topics. The algorithm results in a probability of belonging to each of the established groups.
The main idea of this algorithm is that each document will be assigned to a group, and in turn each group will be assigned to a series of words that are the most relevant or explanatory for that group.
We will see this more clearly in the following images. First of all, we simply associate each word in our corpus (the set of all the words that appear in the texts once we have processed them) to a document, which, a priori, does not provide much information in our classification of the state of the art.
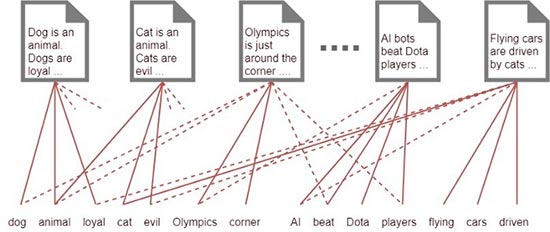
Unless we have a fairly large corpus , we will not be able to process the above information. On the other hand, if we associate each word to a class, group or subject we find a simple way to classify each document and the relationships are much clearer than in the first image.
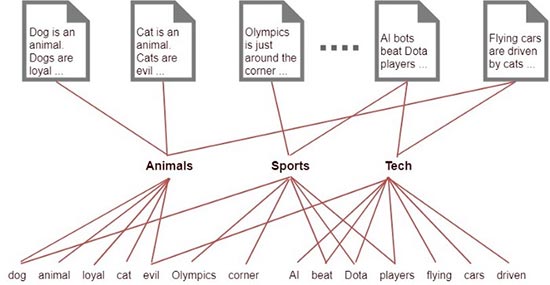
The mathematics behind this algorithm is dense, but we leave that as an exercise for curious readers.
So much for today's application, no doubt with it the librarian would have had things easier and could have saved himself from reading a shelf of chemistry books if they were not of interest to him. There are still other use cases such as the invoice evaluator or the technological publications observatory that we will discuss in the following articles. Don't miss it!












